Soma de vetores: Regra do Paralelogramo e Exercícios resolvidos

A regra do paralelogramo é um princípio fundamental na física e matemática, essencial para a compreensão e manipulação de vetores. Esta regra não apenas simplifica a soma vetorial, mas também estabelece uma base sólida para o estudo de movimentos e forças em diversas áreas da ciência.

Neste artigo, exploraremos detalhadamente o que é a regra do paralelogramo, sua aplicabilidade e como ela se compara a outros métodos de soma vetorial. Através de uma abordagem passo a passo, desvendaremos os mistérios por trás desta regra, oferecendo uma visão clara de seu papel indispensável tanto na física quanto na matemática.

O que é a Regra do Paralelogramo?

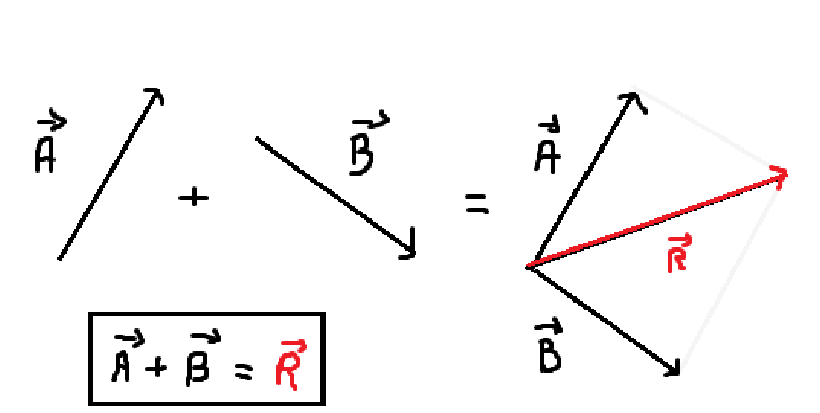
A regra do paralelogramo é um método gráfico utilizado para determinar a soma de dois vetores. Segundo esta regra, dois vetores podem ser somados desenhando-se um paralelogramo, onde os vetores são colocados de maneira que formem dois lados adjacentes do paralelogramo.

A diagonal do paralelogramo que passa pelo ponto de interseção dos vetores então representa a soma vetorial dos dois. Esta técnica não só visualiza a adição de vetores de uma maneira intuitiva, mas também facilita a compreensão da natureza multidirecional das grandezas vetoriais.

Como Utilizar a Regra do Paralelogramo

1. Identificar os Vetores: Escolha os dois vetores que deseja somar. Estes serão os lados adjacentes do paralelogramo.
2. Desenhar o Paralelogramo: Posicione os dois vetores de modo que formem um ângulo, utilizando suas caudas como ponto de partida. A seguir, desenhe linhas paralelas a cada um dos vetores para formar o paralelogramo.
3. Determinar a Diagonal: A diagonal do paralelogramo que parte do ponto comum (onde as caudas dos vetores se encontram) até o ponto oposto representa a soma dos vetores.
4. Medir a Diagonal: Utilizando uma régua ou um software gráfico, meça o comprimento da diagonal. Este será o módulo do vetor soma.
5. Determinar a Direção e Sentido: A direção e o sentido da diagonal representam a direção e o sentido do vetor resultante.

Casos Particulares da Regra do Paralelogramo

A Regra do Paralelogramo abrange diferentes cenários, dependendo do ângulo formado entre os dois vetores. Os casos mais notáveis incluem:

Caso 1: Quando $θ = 0$º

Nesta situação, os vetores estão na mesma direção e sentido, resultando em um vetor soma que é a simples adição de seus módulos.

Caso 2: Quando $θ = 180º$

Aqui, os vetores têm direções iguais, mas sentidos opostos. O vetor soma terá o módulo igual à diferença dos módulos dos vetores originais e direção e sentido do vetor de maior módulo.

Caso 3: Quando $θ = 90º$

Quando os vetores são perpendiculares entre si, o vetor soma pode ser calculado usando o Teorema de Pitágoras, com o vetor resultante formando a hipotenusa do triângulo retângulo.

Métodos Alternativos de Soma Vetorial

Além da Regra do Paralelogramo, existem outros métodos para a soma vetorial, sendo o Método da Linha Poligonal um dos mais utilizados. Cada método tem suas particularidades e pode ser mais conveniente dependendo do contexto ou da complexidade do problema em questão.

Método da Linha Poligonal

O Método da Linha Poligonal, também conhecido como método do triângulo ou método da cadeia, é particularmente útil para somar três ou mais vetores. Este método é aplicado desenhando-se os vetores em sequência, de modo que a cauda de cada vetor subsequente inicie no ponto da cabeça do vetor anterior. O vetor soma é então representado por um vetor que se estende da cauda do primeiro vetor até a cabeça do último vetor na sequência.

1. Sequência dos Vetores: Organize os vetores em uma sequência lógica.
2. Desenho em Cadeia: Desenhe o primeiro vetor e, em seguida, posicione o segundo vetor com sua cauda na cabeça do primeiro. Repita este processo para todos os vetores na sequência.
3. Vetor Resultante: Desenhe um vetor da cauda do primeiro vetor até a cabeça do último vetor. Este será o vetor soma.

Exercícios de Aplicação

Exercício 1

(PUC-RJ) Os ponteiros de hora e minuto de um relógio suíço têm, respectivamente, 1 cm e 2 cm. Supondo que cada ponteiro do relógio é um vetor que sai do centro do relógio e aponta na direção dos números na extremidade do relógio, determine o vetor resultante da soma dos dois vetores correspondentes aos ponteiros de hora e minuto quando o relógio marca 6 horas.

a) O vetor tem módulo 1 cm e aponta na direção do número 12 do relógio.

b) O vetor tem módulo 2 cm e aponta na direção do número 12 do relógio.

c) O vetor tem módulo 1 cm e aponta na direção do número 6 do relógio.

d) O vetor tem módulo 2 cm e aponta na direção do número 6 do relógio.

e) O vetor tem módulo 1,5 cm e aponta na direção do número 6 do relógio.

Para resolver essa questão, precisamos pensar nos vetores como setas que representam os ponteiros do relógio. A posição dos ponteiros nos dá a direção de cada vetor. No caso das 6 horas:

• O ponteiro das horas aponta para o número 6. Podemos considerar esse vetor como tendo direção para baixo no relógio.
• O ponteiro dos minutos aponta para o número 12, que é exatamente na direção oposta ao ponteiro das horas, ou seja, para cima.

O ponteiro das horas tem um comprimento (ou módulo) de 1 cm, e o ponteiro dos minutos tem um comprimento de 2 cm.

Se representarmos o movimento para cima como positivo e o movimento para baixo como negativo (ou vice-versa, o importante é a consistência), podemos tratar a questão como a soma de dois vetores com direções opostas.

Assim:

• O vetor do ponteiro das horas pode ser representado como -1 cm (para baixo).
• O vetor do ponteiro dos minutos pode ser representado como +2 cm (para cima).

Ao somá-los, estamos basicamente subtraindo 1 cm de 2 cm, porque eles estão em direções opostas. Isso nos dá um vetor resultante de 1 cm para cima, na direção do número 12 do relógio.

Portanto, a resposta correta é a alternativa A

Exercício 2

(UDESC) Um "calouro" do Curso de Física recebeu como tarefa medir o deslocamento de uma formiga que se movimenta em uma parede plana e vertical. A formiga realiza três deslocamentos sucessivos:

1. um deslocamento de 20 cm na direção vertical, parede abaixo;
2. um deslocamento de 30 cm na direção horizontal, para a direita;
3. um deslocamento de 60 cm na direção vertical, parede acima.

No final dos três deslocamentos, podemos afirmar que o deslocamento resultante da formiga tem módulo igual a: a) 110 cm b) 50 cm c) 160 cm d) 10 cm

Para resolver essa questão, devemos considerar os três deslocamentos como vetores e usar a regra do paralelogramo para encontrar o vetor deslocamento resultante. Aqui está o passo a passo:

1. Deslocamento 1: 20 cm para baixo (direção vertical).
2. Deslocamento 2: 30 cm para a direita (direção horizontal).
3. Deslocamento 3: 60 cm para cima (direção vertical).

Primeiro, somamos os deslocamentos verticais. Como um é para baixo e o outro para cima, subtraímos 20 cm de 60 cm, resultando em um deslocamento vertical líquido de 40 cm para cima.

Portanto, os deslocamentos efetivos que precisamos considerar para encontrar o vetor resultante são:

• Vertical: 40 cm para cima.
• Horizontal: 30 cm para a direita.

Agora, usamos a regra do paralelogramo, que, neste caso simples, significa que vamos aplicar o Teorema de Pitágoras para encontrar o módulo do vetor resultante, já que os deslocamentos vertical e horizontal formam um triângulo retângulo.

O vetor resultante $R$ é a hipotenusa do triângulo, cujos lados são os deslocamentos horizontal e vertical. Assim:

Portanto, o deslocamento resultante da formiga tem módulo igual a 50 cm, o que corresponde à alternativa B.

Para acabar

Eai, achou fácil? Essa é uma das matérias que mais caem no vestibular. Mas não se engane, dominar física ou qualquer outra matéria do vestibular vai além de entender um único problema. É aqui que entra o VestCards, uma ferramenta inovadora projetada para transformar sua preparação para o vestibular.

Com o VestCards, a revisão se transforma em um jogo, onde aprender se torna uma atividade mais natural e eficaz. Imagine ter acesso a um método de estudo que realmente faz com que o conteúdo permaneça em sua memória. 🧠 Isso é o que o VestCards oferece, com decks abrangendo todos os temas essenciais para o ENEM e outros vestibulares, incluindo matemática, física, química, biologia, e muito mais.

E a melhor parte? Você pode começar agora mesmo, com acesso a mais de 40 decks gratuitos na plataforma. Cada deck, como o de Funções I (1º e 2º graus) que é GRÁTIS, é cuidadosamente elaborado para cobrir os conceitos-chave, fórmulas e questões que frequentemente aparecem nos exames. É a ferramenta perfeita para otimizar seus estudos, permitindo que você revise de maneira eficiente e eficaz.

Não perca a oportunidade de elevar sua preparação para o próximo nível. Cadastre-se no VestCards hoje mesmo e descubra uma nova maneira de estudar. É totalmente gratuito para começar, e você tem a opção de explorar ainda mais recursos com um teste de 7 dias com direito a reembolso, caso não atenda às suas expectativas.

Prepare-se para o sucesso nos vestibulares com o VestCards. Sua jornada rumo à aprovação no vestibular começa aqui. 🚀🧡