Área e Volume da Esfera: Fórmula e Exercícios ENEM e FUVEST

O que é uma Esfera?

A esfera é uma figura geométrica tridimensional perfeitamente simétrica, em que todos os pontos da superfície estão à mesma distância de um ponto central, conhecido como centro da esfera. Essa distância constante é chamada de raio da esfera.

Podemos imaginar a esfera como a forma de objetos comuns, como uma bola de futebol ou uma laranja. Diferente de um círculo, que é uma figura plana, a esfera possui volume, ocupando um espaço no ambiente tridimensional. ⚽

Definição e Características da Esfera

A esfera é definida como o conjunto de todos os pontos no espaço que estão a uma distância fixa (raio) de um ponto central. Algumas características importantes da esfera incluem:

• Centro: O ponto central da esfera, de onde todas as distâncias são medidas.
• Raio ($r$): A distância do centro até qualquer ponto na superfície da esfera.
• Diâmetro ($d$): A maior distância entre dois pontos na superfície da esfera, passando pelo centro. É o dobro do raio ($d = 2r$).
• Superfície Esférica: A área externa da esfera.

Como Calcular a Área da Esfera?

Calcular a área da superfície de uma esfera é um passo fundamental na geometria espacial. A área da esfera refere-se à medida da superfície externa que a compõe, e sua fórmula é derivada com base em conceitos geométricos. 👀

Fórmula da Área da Esfera

A fórmula para calcular a área da superfície de uma esfera é:

Onde:

• $A$ é a área da esfera.
• $r$ é o raio da esfera.
• $\pi$ (pi) é uma constante matemática que aproximadamente vale 3,14159.

Essa fórmula nos diz que a área da esfera é quatro vezes a área de um círculo cujo raio é igual ao da esfera.

Passo a Passo do Cálculo

Vamos entender como aplicar essa fórmula com um exemplo prático.

1. Identifique o raio da esfera ($r$): Primeiramente, você precisa determinar o valor do raio da esfera. Se, por exemplo, o raio for 5 cm, esse será o valor de $r$ que utilizaremos na fórmula.
2. Eleve o raio ao quadrado ($r²$): Em seguida, eleve o valor do raio ao quadrado. No nosso exemplo:

3. Multiplique por $4\pi$: Agora, multiplique esse resultado por $4\pi$:

Portanto, a área da superfície da esfera com raio de 5 cm é 314,159 cm². Esse método pode ser aplicado para qualquer esfera, bastando ajustar o valor do raio na fórmula.

Como Calcular o Volume da Esfera?

Assim como a área da superfície, o cálculo do volume de uma esfera é essencial na geometria. O volume de uma esfera representa o espaço tridimensional ocupado por ela. Para calcular esse volume, utilizamos uma fórmula específica.

Fórmula do Volume da Esfera

A fórmula para calcular o volume de uma esfera é:

Onde:

• $V$ é o volume da esfera.
• $r$ é o raio da esfera.
• $\pi$ (pi) é a constante matemática, aproximadamente igual a 3,14159.

Essa fórmula mostra que o volume de uma esfera é diretamente proporcional ao cubo do raio, multiplicado por $\frac{4}{3}$ e por $π$.

Passo a Passo do Cálculo

Vamos aplicar a fórmula do volume com um exemplo prático para entender melhor o processo:

1. Determine o raio da esfera ($r$): Assim como no cálculo da área, o primeiro passo é identificar o valor do raio. Suponha que o raio da esfera seja 6 cm.

2. Eleve o raio ao cubo ($r³$): Em seguida, eleve o raio ao cubo, ou seja, multiplique o valor do raio por ele mesmo três vezes:

   $$r^3 = 6^3 = 216 \, \text{cm}^3$$

3. Multiplique por $\frac{4}{3}\pi$: Agora, multiplique o resultado por $\frac{4}{3}π$:

   $$V = \frac{4}{3} \times 3,14159 \times 216 \, \text{cm}^3 = 904,32 \, \text{cm}^3$$

Portanto, o volume da esfera com raio de 6 cm é 904,32 cm³. Esse processo pode ser aplicado a qualquer esfera, bastando substituir o valor do raio na fórmula.

Resoluções de questões sobre esferas

Questão 01

(ENEM) Uma empresa que fabrica esferas de aço, de 6 cm de raio, utiliza caixas de madeira, na forma de um cubo, para transportá-las. Sabendo que a capacidade da caixa é de 13.824 cm³, então o número máximo de esferas que podem ser transportadas em uma caixa é igual a

A) 4

B) 8

C) 16

D) 24

E) 32

Primeiro, calculamos o volume de uma esfera com raio de 6 cm usando a fórmula: $V = \frac{4}{3} \pi r^3$

Substituindo o valor do raio, obtemos $V = \frac{4}{3} \times 3,14159 \times 216 = 904,32 \, \text{cm}^3$. Isso significa que o volume de cada esfera é 904,32 cm³.

Em seguida, dividimos o volume total da caixa (13.824 cm³) pelo volume de uma esfera para determinar quantas esferas caberiam teoricamente. Essa divisão nos dá aproximadamente 15,28 esferas. Contudo, como o número de esferas deve ser inteiro, inicialmente consideramos que caberiam 15 esferas na caixa.

No entanto, é importante considerar o formato da caixa e a disposição das esferas dentro dela. Como a caixa é cúbica e as esferas devem ser organizadas de forma eficiente, calculamos o comprimento do lado da caixa ($l$) extraindo a raiz cúbica do volume:

Dessa forma, o $l$ resultante é de 24 cm. Sabendo que o diâmetro de cada esfera é 12 cm (2 vezes o raio), verificamos quantas esferas cabem ao longo de um lado da caixa. Como 24cm dividido por 12 cm resulta em 2 esferas por lado, podemos arranjar 2 esferas em cada direção (comprimento, largura e altura), totalizando $2 \times 2 \times 2 = 8$ esferas.

Portanto, o número máximo de esferas que podem ser transportadas na caixa é 8. A resposta correta é B) 8.

Questão 02

(FUVEST) Um recipiente cilíndrico, cujo raio da base é 6 cm, contém água até uma certa altura. Uma esfera de aço é colocada no interior do recipiente, ficando totalmente submersa. Se a altura da água subiu 1 cm, então o raio da esfera é:

A) 1 cm
B) 2 cm
C) 3 cm
D) 4 cm
E) 5 cm

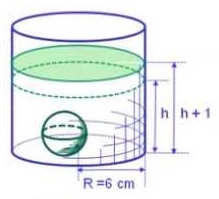
Primeiro, vamos considerar o volume da água deslocada pela esfera, que corresponde ao volume da esfera. O volume da água deslocada pode ser expresso como o volume de um cilindro com altura de 1 cm e raio da base de 6 cm.

O volume $V_1$ da água deslocada é dado por:

Substituindo o valor do raio $r = 6$ cm:

Este é o volume da esfera, pois a esfera submersa faz com que o volume de água deslocado seja equivalente ao volume da própria esfera.

Sabemos que o volume $V_2$ da esfera é dado por:

Agora, igualamos esse volume ao volume de água deslocado $36\pi$:

Podemos simplificar a equação dividindo ambos os lados por $\pi$:

Agora, multiplicamos ambos os lados por 3/4 para eliminar a fração:

Para encontrar o valor de $r$, tomamos a raiz cúbica de 27:

Portanto, o raio da esfera é 3 cm, que corresponde à alternativa c) 3 cm.

Questão 03

(ENEM) Uma indústria de perfumes embala seus produtos, atualmente, em frascos esféricos de raio R. Observou-se que haverá redução de custos se forem utilizados frascos cilíndricos com raio da base r/3, sendo h a altura da nova embalagem.
Para que seja mantida a mesma capacidade do frasco esférico, a altura do frasco cilíndrico (em termos de R) deverá ser igual a

A) 2R

B) 4R

C) 6R

D) 9R

E) 12R

Para resolver a questão, comparamos o volume do frasco esférico e o volume do frasco cilíndrico. O volume da esfera é dado por $\frac{4}{3} \pi R^3$. O volume do cilindro, com raio $r = \frac{R}{3}$ e altura $h$, é $\pi \left(\frac{R}{3}\right)^2 \cdot h$. Igualando os volumes e simplificando:

Eliminando $\pi$ e resolvendo para $h$:

Portanto, a altura $h$ do cilindro deve ser $12R$. A resposta correta é E) 12R.

Aplicações Práticas da Área e Volume da Esfera no Cotidiano

A área e o volume de uma esfera são conceitos fundamentais que aparecem em diversas situações práticas no cotidiano e em várias áreas do conhecimento. Por exemplo, na indústria, as fórmulas de volume são essenciais para calcular a capacidade de recipientes esféricos, como tanques de armazenamento de líquidos ou frascos de perfumes, garantindo o uso eficiente dos materiais e espaço.

Já para a área, um exemplo prático é encontrado na fabricação de rolamentos esféricos, que são fundamentais para a redução do atrito em máquinas e motores, aumentando a eficiência e a durabilidade dos equipamentos. Esses cálculos também são cruciais na arquitetura e construção civil, especialmente em projetos que envolvem cúpulas e superfícies esféricas, onde o cálculo preciso da área e volume garante a integridade estrutural e a funcionalidade do design.

Para terminar

Depois de explorar o fascinante universo da área e do volume das esferas, é claro que esses conceitos vão além da teoria, encontrando aplicação em diversas áreas do nosso cotidiano e em muitos campos de estudo. Compreender a geometria esférica é essencial não só para resolver problemas matemáticos, mas também para enfrentar os desafios práticos de diversas profissões e setores. 🏀

E aí, acha que essa jornada te ajudou? Se você gostou de mergulhar nesses conceitos, imagine poder revisar de forma dinâmica e eficiente todo o conteúdo de Matemática e outras matérias para o vestibular. Com VestCards, a preparação para o ENEM e outros vestibulares se torna mais interativa e eficaz. Ao invés de uma rotina de estudos cansativa, você transforma o aprendizado em um jogo, mantendo a matéria fresca na sua mente.

Tudo o que vimos aqui sobre geometria esférica está bem explicado nos decks da VestCards de Geometria Espacial, junto com todos os outros conteúdos essenciais para o ENEM e vestibulares como a Fuvest e a Unicamp. Confira nossos decks gratuitos de Matemática e muito mais! Imagine ter um baralho de flashcards inteligentes, que sabem exatamente o que você precisa revisar e quando. Essa é a mágica do VestCards! Cadastre-se agora e ganhe acesso a mais de 40 decks gratuitos na plataforma. Estamos te esperando para tornar sua preparação mais leve e eficaz! 🧡